La nature quantique de l’électron et les orbitales atomiques
Généralisation : la description de l’objet quantique par la notion d’état ou « ket »
La liaison chimique élémentaire : molécule H2+
Etats électroniques dans le solide élémentaire
Les atomes sont constitués d’un noyau (protons et neutrons en interaction forte) et d’électrons. Les protons ont une charge électrique « positive », les électrons ont une charge électrique opposée, « négative », par convention. Les électrons sont en interaction électrostatique avec le noyau, on dit aussi interaction coulombienne. Ils sont attirés par le noyau : c’est fondamentalement leur nature quantique qui explique qu’ils ne s’effondrent pas tous sur le noyau (auquel cas toute la matière se réduirait à un point !). A très, très petite échelle : l’échelle élémentaire, l’échelle des « grains » de matière, ceux-ci (électrons, protons…) se comportent à la fois comme des particules et comme des ondes. De cette nature duale découlent les principes qui expliquent la stabilité de l’édifice atomique et la cohésion de la matière. Nous n’entrerons pas dans ces principes mais il est utile de se former une compréhension de la nature quantique des électrons, car la distribution des différents états quantiques électroniques est à la base de propriétés essentielles de la matière (structure, réactivité, propriétés physiques…).
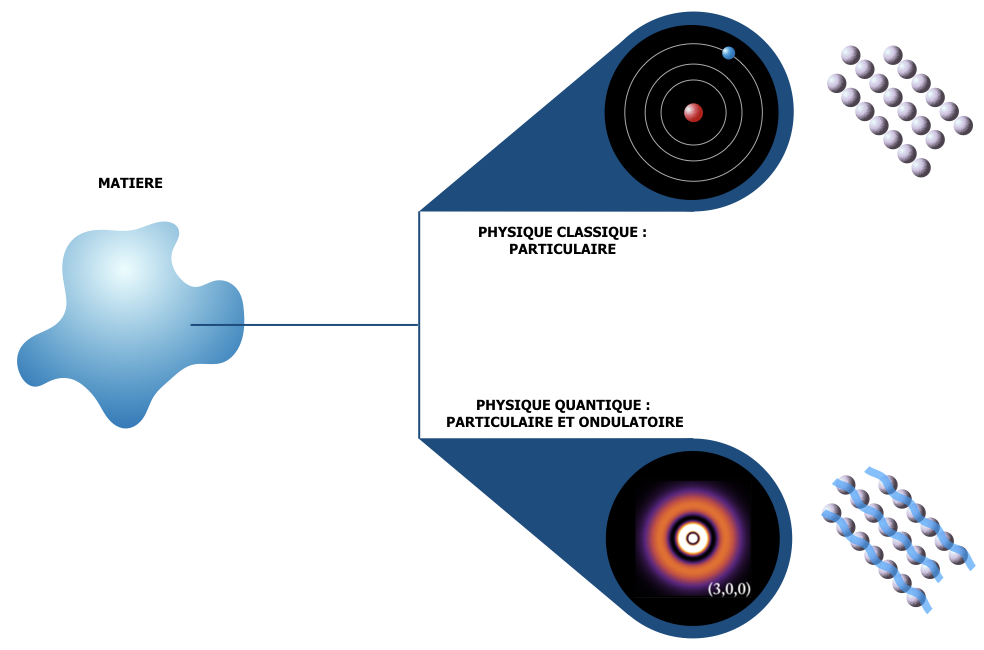
La nature quantique de l’électron et les orbitales atomiques
Dans notre monde macroscopique, il est possible, en utilisant les forces appropriées, d’impulser un mouvement à un objet (translation, vibration, rotation) avec n’importe quelle vitesse et lui conférer ainsi n’importe quelle énergie. Connaissant la position et la vitesse de départ et les forces appliquées, il est ensuite possible de déterminer la trajectoire et la vitesse de l’objet à tout instant avec toute la précision voulue.
Tout cela n’est plus possible à l’échelle des atomes, où les masses sont très faibles et les transferts d’énergie sont minimes. Cette échelle est celle des grains ou « quantas » : particules de matières et quantas d’énergie. L’invalidité des principes de base de la physique classique (celle du monde macroscopique) aux objets microscopiques s’est révélée au cours du 19è siècle. Il était impossible d’expliquer le spectre du corps noir dans le domaine des courtes longueurs d’onde, ni la capacité calorifique de la matière à basse température, ni le caractère discret des spectres atomiques ou moléculaires. Ces trois phénomènes nécessitent de postuler la quantification de l’énergie absorbée ou émise, ce qu’on fait Planck, Einstein et Bohr au début du 20è siècle. Puis, les conséquences en seront d’admettre une description probabiliste des particules de matière, en termes de fonctions d’onde ou d’« états » quantiques.
Deux grandes étapes ont amené à l’idée des orbitales atomiques, ces fonctions d’onde qui décrivent l’électron dans l’atome et sont associées à des énergies bien déterminées.
Etape de la quantification : le modèle de Bohr
L’atome d’hydrogène est le plus simple de la nature puisqu’il est constitué d’un proton et d’un électron. Les raies émises par un tube à décharge contenant de l’hydrogène sont extrêmement fines.

Spectre atomique de l’hydrogène. SlidePlayer – Le spectre de l’hydrogène, par Claudette Prigent.
Pour expliquer cela, Bohr postule que l’électron ne peut occuper que certaines orbites autour du noyau. Les raies du spectre correspondent aux photons émis lorsque l’électron transite d’une orbite plus haute en énergie à une orbite plus basse en énergie :
hν = I Efinale – Einitiale I
Les orbites autorisées sont les orbites pour lesquelles le moment cinétique est un multiple de la constante h : L=nh, n = 1, 2, 3, … Ce postulat permet de calculer avec une très grande précision le spectre expérimental de l’hydrogène.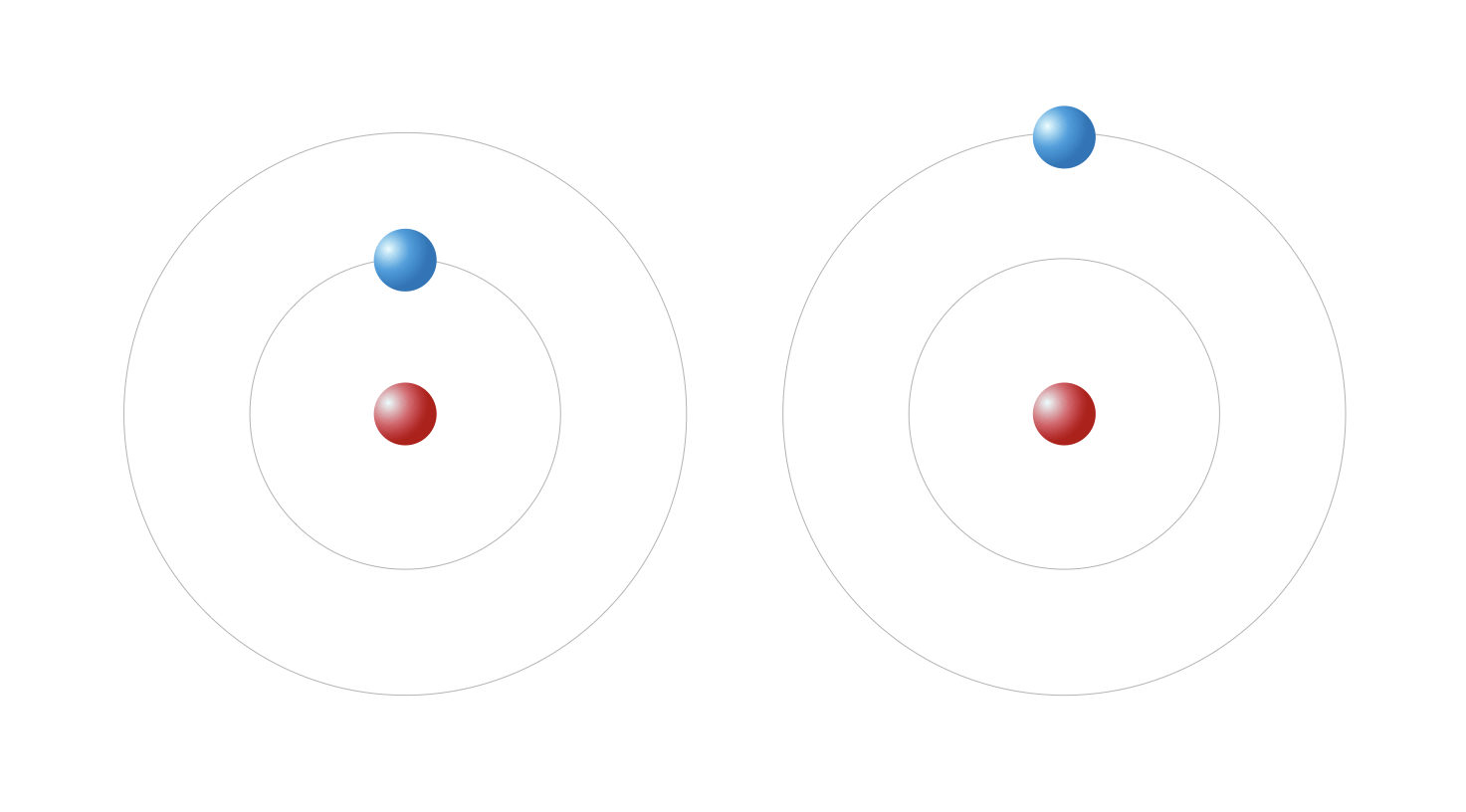
L’électron de l’hydrogène selon le modèle de Bohr dans deux orbites différentes
C’est de Broglie qui donne une interprétation de la quantification du moment cinétique : l’électron est une onde. Par analogie avec les photons, son énergie est E=hν et son impulsion est p= me×vitesse= h où me est la masse, ν est la fréquence et λ est la longueur d’onde de l’électron. La constante h (avec h=h2π ) est la constante de Planck, dont la valeur a été déterminée expérimentalement à partir du spectre du corps noir. Les orbites stables sont les orbites stationnaires où la circonférence est égale à n fois la longueur d’onde : 2πr=nλ. Le moment cinétique est alors bien quantifié en nh :
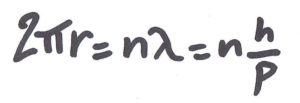
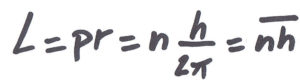
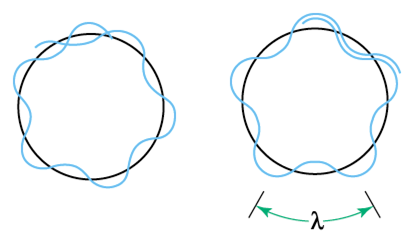
A gauche : orbite non permise, à droite : orbite permise. Dessin de Claudette Prigent (SlidePlayer – Le spectre de l’hydrogène)
Etape des probabilités : la fonction d’onde
Le modèle de Bohr est très vite critiqué : il est en totale contradiction avec les lois de l’électrodynamique, qui imposent que l’électron perde son énergie par rayonnement et finisse par s’effondrer en spirale sur le noyau. Il s’avère aussi impossible d’observer la trajectoire de l’électron expérimentalement.
Le modèle de Bohr est en fait imprégné, ancré dans la vision classique née de l’observation du monde macroscopique. C’est en abandonnant cette vision qu’on a pu surmonter les incohérences. Ainsi, la vision classique de la particule avec sa trajectoire a été remplacée par la notion d’onde de probabilité, appelée aussi fonction d’onde. La ligne orbitalaire noire du dessin ci-dessus est remplacée par une enveloppe délimitant le domaine de l’espace où l’électron a une forte probabilité d’être présent (par exemple : 90% « de chance d’être là »). Cette probabilité de présence est le module au carré de la fonction d’onde, fonction complexe donnant l’amplitude de probabilité de trouver l’électron en tout point de l’espace. Les fonctions d’onde stationnaires des électrons dans l’atome sont appelées orbitales atomiques.
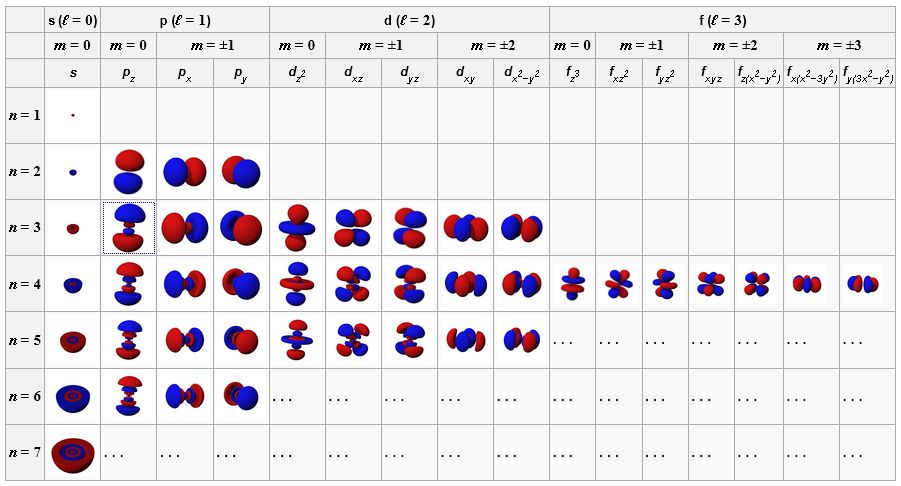
Les orbitales atomiques, fonctions d’onde stationnaires de l’électron dans l’atome, selon les 3 nombres quantiques n, l, m qui les caractérisent. La couleur bleue ou rouge indique le signe, positif ou négatif, de la fonction d’onde. L’enveloppe de ces orbitales délimite le domaine de présence de l’électron. (Dhatfield Wikimedia Commons).
Les orbitales atomiques dépendent de 3 nombres quantiques : n, l et m. Les nombres l et m caractérisent le moment cinétique (sa valeur et sa direction), le nombre n est relié à l’énergie.
La notion de fonction d’onde est générale, elle s’applique pour décrire tous les électrons : ceux liés à un noyau, ou à plusieurs noyaux, ou ceux extraits de leurs atomes et partis « en voyage » comme dans un faisceau électronique. La fonction d’onde est tout ce qu’on peut connaître sur l’électron : elle donne la probabilité de trouver l’électron dans un certain coin de l’espace, et la probabilité que sa vitesse soit dans un certain intervalle. La nature ondulatoire fait qu’il est impossible de connaitre à la fois la position et la vitesse de l’électron avec autant de précision qu’on voudrait : on ne peut pas réduire l’électron à une particule se déplaçant dans l’espace. Ce constat fondamental est formulé dans les relations d’incertitude d’Heisenberg :
∆r ∆p≥h/2 où Δr et Δp sont les écart-types sur la mesure de la position r et de l’impulsion p (= m *vitesse) de l’électron.
Généralisation : la description de l’objet quantique par la notion d’état ou « ket »
Une étape supplémentaire a été franchie quand on a compris qu’il était inutile de chercher à représenter les systèmes microscopiques par des points ou même par des enveloppes de probabilité. Pourquoi ne pas considérer l’état de ces systèmes comme des grandeurs abstraites, et simplement chercher à relier ces états à des grandeurs mesurables ? Car on ne peut vouloir connaitre et prédire que des grandeurs mesurables, tout le reste est fantasme inutile.
Le formalisme de la mécanique quantique repose sur cette idée que les systèmes microscopiques (un électron, une assemblée d’électrons, un atome, une molécule, etc) sont dans un certain état quantique, appelé « ket », appartenant à l’ « espace des états possibles ». Le résultat de la mesure de toute grandeur physique se représente par l’action d’un opérateur sur cet état.
Par exemple, considérons une molécule A-B dont on mesure l’énergie cinétique de vibration. Nous admettons que cette énergie est quantifiée avec un nombre quantique n sous la forme En=hν(n+1/2) où ν est la fréquence propre de vibration. Le résultat de la mesure donne 7/2 hν. On peut dire que la molécule est maintenant dans l’état n = 3. Mais avant la mesure, quel était cet état ? Il faut prendre une autre molécule dans le même état initial et faire une autre mesure. On trouve alors 3/2 hν. Reprenons encore une autre molécule, mesurons, notons le résultat. On voit que c’est au bout d’un grand nombre de mesures sur un grand nombre de molécules préparées dans le même état, qu’on pourra connaître l’énergie de cet état : on donnera les différents résultats de mesure, avec pour chacun une probabilité. C’est l’ensemble de ces probabilités qui caractérise l’état de la molécule. Les différentes valeurs possibles de l’énergie et les états propres associés (états « n » dont l’énergie est à coup sûr « En ») caractérisent l’opérateur « énergie cinétique de vibration ».
Les objets quantiques sont donc définis par des probabilités. Ce sont les valeurs moyennes, déterminées sur un très grand nombre de ces objets, qui font le lien avec le monde macroscopique : ces valeurs moyennes (énergie, position, etc) se comportent selon les lois de la physique « classique ».
La liaison chimique élémentaire : molécule H2+
Dans un atome de numéro atomique Z, nous avons Z électrons qui se répartissent dans les orbitales atomiques à raison de 2 électrons par orbitale n, l, m. La loi sous-jacente à ce remplissage est le principe d’exclusion de Pauli : 2 électrons ne peuvent pas exister dans exactement le même état quantique. Or un état quantique monoélectronique est caractérisé par n, l, m mais aussi s et ms, les nombres quantiques associés au moment cinétique de spin. Pour un électron, s = ½, et ms peut prendre 2 valeurs : ½ et -1/2. L’état de l’électron est donc caractérisé par n, l, m, s (=1/2) et ms et on a au maximum 2 électrons par orbitale n, l, m : celui avec ms = ½ et celui avec ms = -1/2.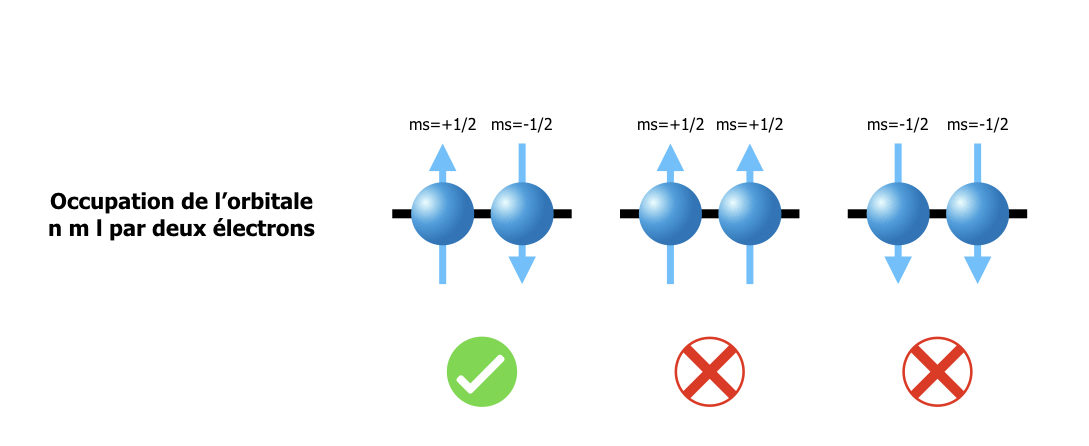
Principe d’exclusion de Pauli
Les électrons les plus hauts en énergie (n le plus grand) sont aussi les plus externes : ce sont eux qui forment les liaisons chimiques. Ils sont appelés électrons de valence. La molécule H2+, formée de 2 noyaux d’hydrogène et d’un électron, est le cas le plus simple pour étudier la formation de la liaison chimique.
Considérons 2 noyaux d’hydrogène Ha et Hb et un électron. Si les noyaux Ha et Hb sont très loin l’un de l’autre, l’électron est soit sur le noyau Ha, soit sur le noyau Hb. Le système de nos 3 particules a donc deux états électroniques possibles : l’état 1 où l’électron est sur Ha, et l’état 2 où il est sur Hb. Par symétrie, ces 2 états ont la même énergie. Lorsque les 2 noyaux se rapprochent, l’électron situé sur un noyau ressent l’attraction coulombienne par l’autre noyau. Il est « transféré » sur l’autre noyau de sorte qu’il ne sait plus à quel atome il appartient. Cela donne naissance à deux nouveaux états, les états moléculaires « + » et « – ». En terme ondulatoire, l’état + correspond à l’interférence constructive des fonctions d’onde 1 et 2 qui s’additionnent en phase, renforçant la probabilité de présence, ie la densité électronique, entre les 2 noyaux. L’état – correspond à la situation d’interférence destructive : les 2 fonctions d’onde s’additionnent en opposition de phase, détruisant la probabilité de présence entre les noyaux.
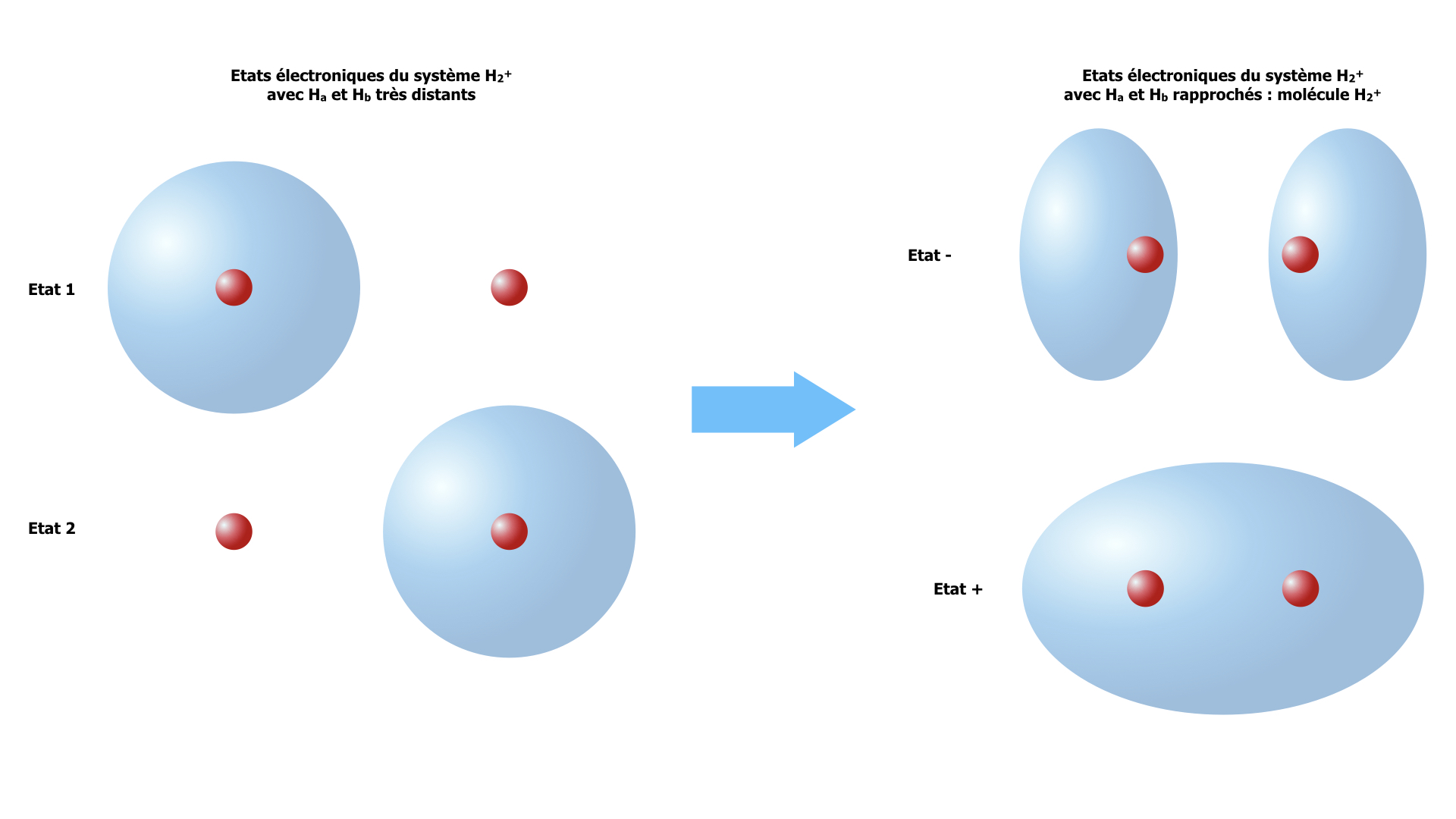
Formation des deux états moléculaires « + » et « – » de la molécule H2+ par combinaison des états 1 et 2 formés par les deux atomes séparés.
Dans l’état +, l’électron bénéficie de l’attraction par les 2 noyaux. Il est stabilisé : son énergie est plus basse que dans les états 1 ou 2. Comme sa probabilité de présence est forte entre les noyaux, il sert de « ciment » aux 2 noyaux : l’état + est donc appelé « état liant ». Par opposition, l’état – où l’électron est essentiellement situé à l’extérieur de l’espace internucléaire est appelé « état antiliant », son énergie est plus élevée. L’énergie des états + et – est représentée dans un diagramme des niveaux d’énergie (monoélectronique) de la molécule. Le paramètre β est l’intégrale de résonance, qui mesure l’effet énergétique du couplage entre les 2 états 1 et 2 permettant le transfert de l’électron.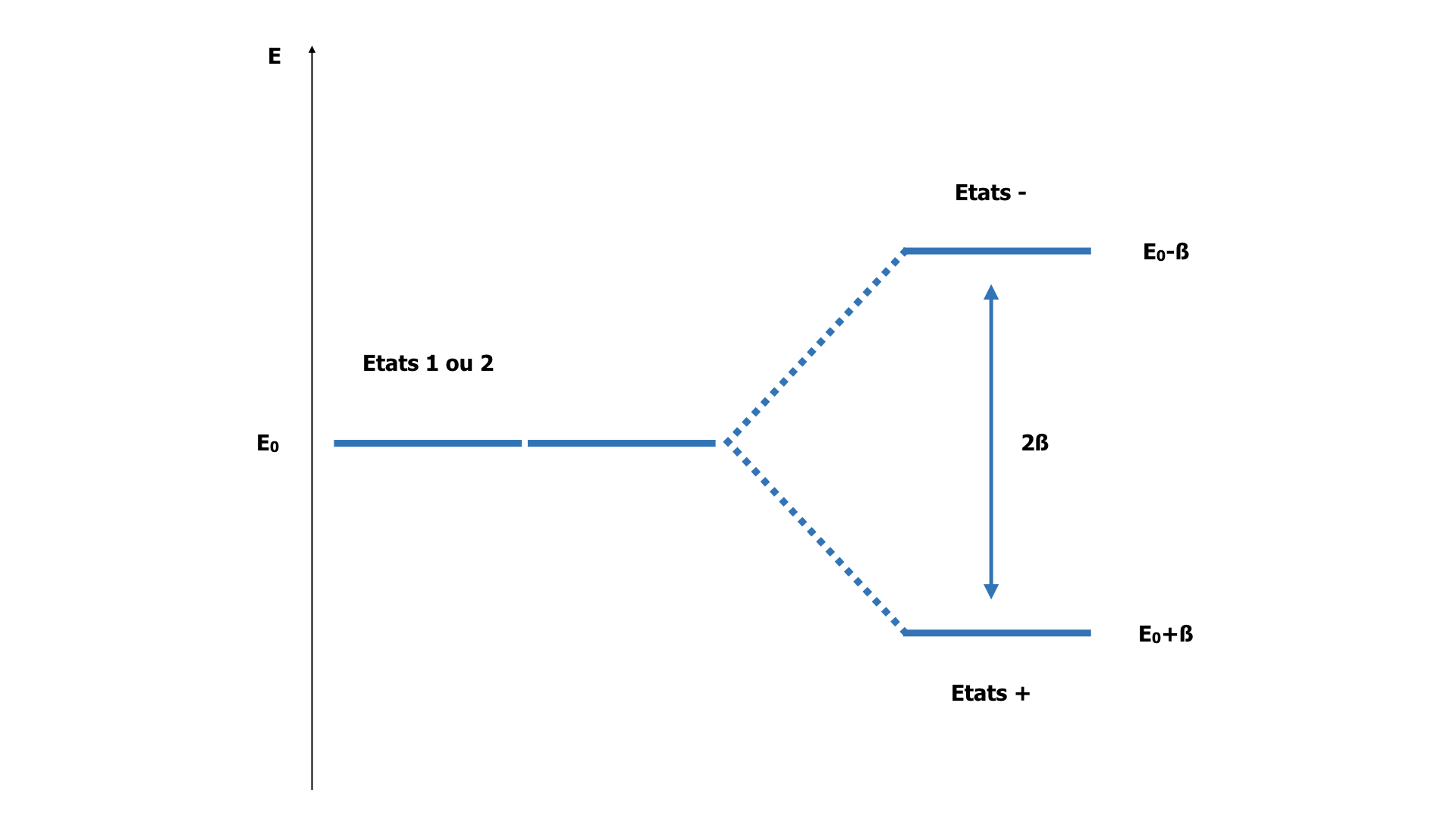
Les fonctions d’onde associées aux états moléculaires + et – sont appelées orbitales moléculaires, OM. Comme on vient de le faire très qualitativement pour le dihydrogène, on les détermine en procédant à la combinaison linéaire des orbitales atomiques des électrons de valence. Dans le couplage entre deux états atomiques, plus le recouvrement entre les deux orbitales atomiques est grand et plus le paramètre énergétique β est important. Dans les molécules, les atomes s’arrangent donc pour maximiser les recouvrements de leurs OA, générant des structures moléculaires bien définies.
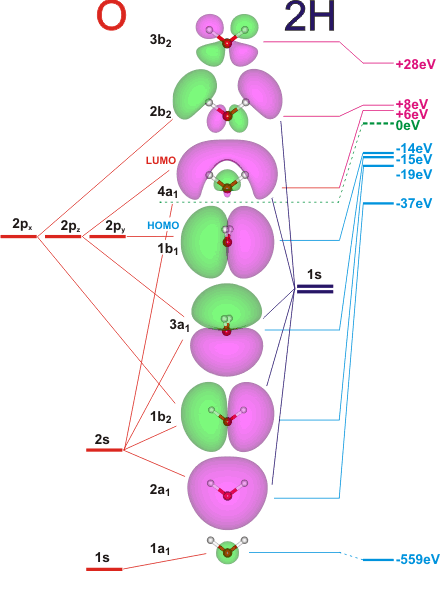
Orbitales moléculaires de la molécule d’eau, H2O (http://www1.lsbu.ac.uk/water/h2o_orbitals.html).
Les orbitales atomiques de valence sont les OA 1s(H1), 1s(H2), et 1s(O), 2s(O), 2px(O), 2py(O) et 2pz(O).
Il y a 10 électrons de valence dans l’édifice, qui se placent dans les 5 OM de plus basse énergie : 1a1, 2a1, 1b2, 3a1 et 1b1. Les dénominations a1, b1… indiquent le type de symétrie de l’OM.
Etats électroniques dans le solide élémentaire
Et si l’électron était en interaction non pas avec 2 noyaux, mais avec un très grand nombre N de noyaux ? C’est le cas du solide, formé d’un nombre d’atomes « infini » dans les 3 directions de l’espace.
Le solide le plus simple peut être imaginé comme une chaîne linéaire de N atomes distants de a. On suppose que dans l’atome isolé, l’électron se trouve dans une OA, par exemple : 1s (n=1, l=0, m=0).
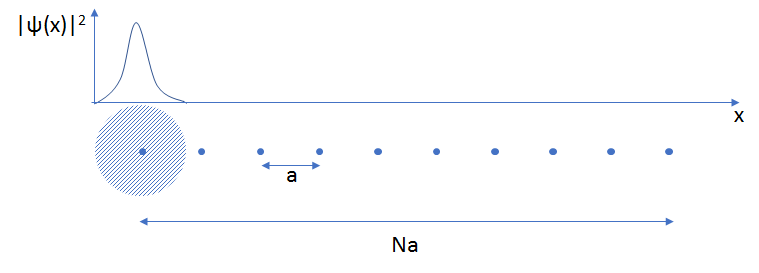
Modèle le plus simple du solide : chaîne linéaire de N atomes espacés de la distance a. Le disque bleu représente la fonction d’onde ψ(x) de l’OA du premier atome (OA de type 1s). Au-dessus, on a tracé le module au carré de la fonction d’onde, |ψ(x)|2 : c’est la probabilité de présence de l’électron à la position x.
Suivant la même analyse qu’avec la molécule H2+, lorsque la distance a est très grande, l’électron est situé dans l’OA du 1er atome, ou du 2ème atome, …, ou du Nème atome. On dit qu’il est localisé. On a affaire à N états électroniques « atomiques »* tous de même énergie.
*On parle ici des états électroniques stationnaires, invariants dans le temps et associés à une des valeurs discrètes de l’énergie. Un état électronique quelconque est une combinaison linéaire de ces états stationnaires (et n’est pas invariant dans le temps). Il est suffisant de connaitre tous les états stationnaires pour connaitre tous les états possibles de l’électron.
Lorsque la distance a diminue, les OA entrent en recouvrement : il y a combinaison (ou couplage) entre les états électroniques atomiques, donnant naissance à d’autres états électroniques où l’électron est cette fois délocalisé sur plusieurs noyaux. Ce sont les états électroniques* du solide.
Le recouvrement entre OA se fait principalement entre atomes voisins, le couplage fait donc apparaître un paramètre énergétique β relatif à la stabilisation ou à la déstabilisation de l’électron selon que la combinaison entre voisins est constructive ou destructive (approximation de Hückel). Par ailleurs, il est très utile de remarquer que ces états électroniques sont invariants par la translation de a : dans une chaîne suffisamment grande d’atomes, une translation de a ne change pas les données énergétiques du problème (l’électron translaté de a voit toujours deux atomes voisins identiques comme avant la translation). Cette propriété de symétrie impose que les fonctions d’onde associées aux états électroniques sont des fonctions périodiques de période Na/n, avec n = 0, 1, …, N.
Ainsi, la combinaison des N états électroniques « atomiques » donne N états électroniques dans le solide, de fonction d’onde périodique avec la période Na/n, avec n = 0, 1, 2, …, N, et dont l’énergie est :
En=E+2βcos(2πnN)
L’état électronique avec n = 0 correspond au cas où tous les couplages 2 à 2 sont constructifs : c’est le cas « totalement liant » où l’électron a une forte probabilité de présence entre les atomes. Son énergie est E + 2β (β est négatif). La fonction d’onde est uniforme sur tout le solide.
L’état électronique avec n = N correspond au cas où, au contraire, tous les couplages sont 2 à 2 destructifs : la probabilité de présence de l’électron est nulle dans l’espace interatomique. C’est l’état « totalement antiliant ». Son énergie est E – 2β et la fonction d’onde associée a pour période a.
Sur le dessin ci-dessous, nous avons également représenté un état intermédiaire (n=4) : la probabilité de présence de l’électron entre les atomes décrit une onde de période Na/4. L’énergie est intermédiaire.
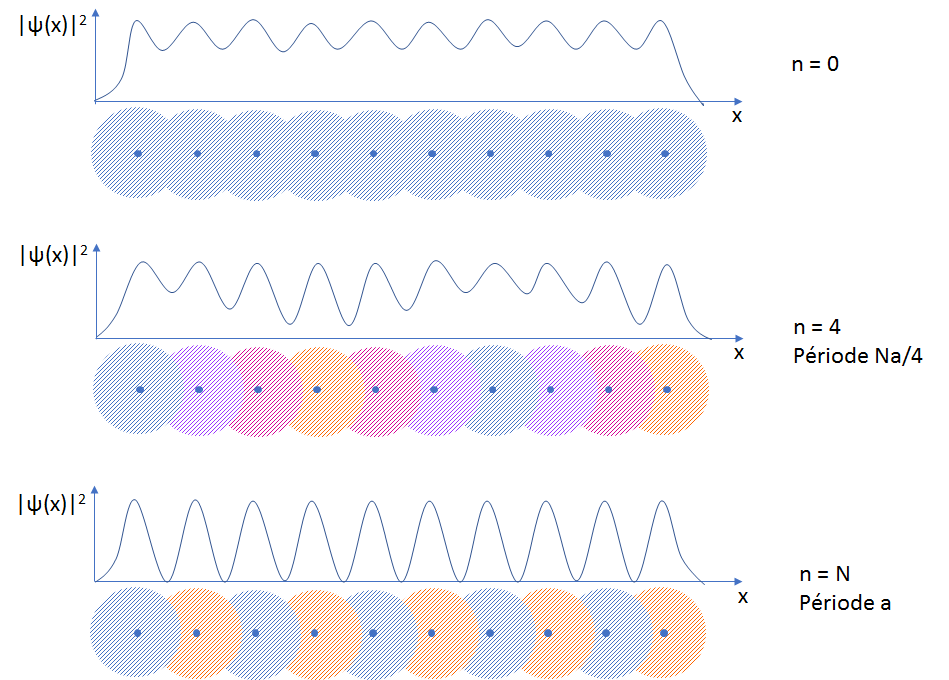
Fonctions d’onde des électrons dans le solide. En bas, les disques représentent ψ(x). Les couleurs représentent le signe de ψ(x) : bleu pour +1, orange pour -1, nuances de violet pour les valeurs complexes intermédiaires entre +1 et -1. En haut, la probabilité de présence |ψ(x)|2 est dessinée en fonction de x.
Lorsque N tend vers l’infini, la différence d’énergie entre 2 états n et n+1 tend vers zéro. Les N niveaux d’énergie deviennent un continuum qu’on appelle une bande. Ainsi, dans un solide, les électrons se distribuent dans des bandes d’énergie issues du couplage de leurs OA. Comme il y a toujours (en dehors de l’hydrogène) plusieurs OA de valence, on a une bande d’énergie par OA de valence. Ces bandes peuvent se recouvrir, ou pas. S’il existe un domaine d’énergie « interdit », couvert par aucune bande, on parle de bande interdite ou « gap » en énergie.
La distribution des électrons dans les bandes détermine les propriétés électriques et optiques du solide.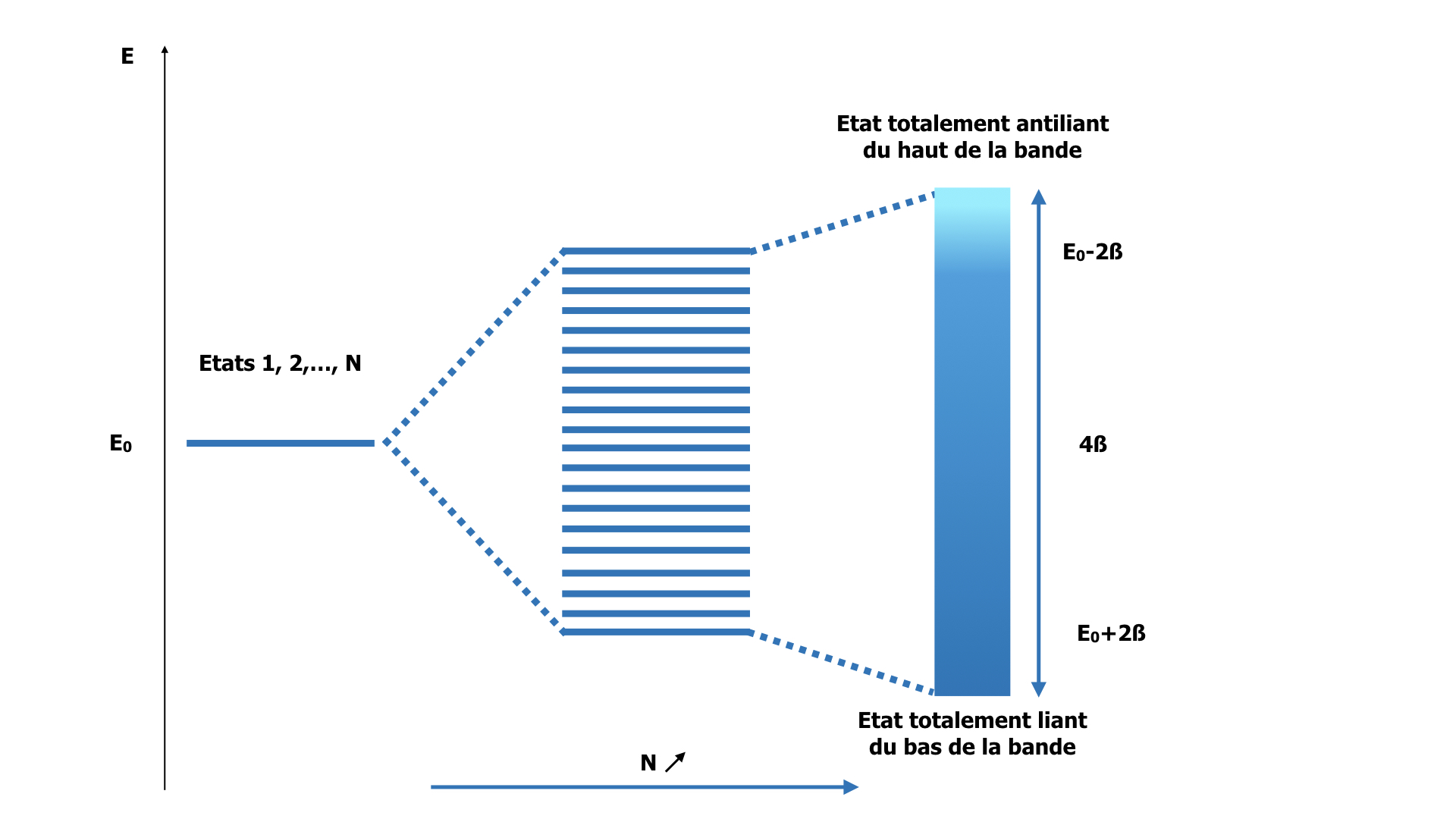
Formation de la bande d’énergie associée au recouvrement des orbitales 1s de notre solide.
