Une phase correspond à un composé avec un domaine de composition chimique et une structure atomique bien définies par les conditions d’équilibre thermodynamique. Tout mélange d’atomes quels qu’ils soient s’arrange en une ou plusieurs phases en équilibre thermodynamique interne et entre elles.
Pour comprendre comment la thermochimie permet de prévoir les phases à l’équilibre, nous décrivons l’exemple le plus simple du mélange à deux corps, ce qui nous donne l’occasion de présenter deux outils très utiles aux chimistes : le potentiel chimique et les diagrammes de phase. Différents matériaux sont décrits en termes de leurs phases constitutives dans les pages « matières et matériaux ».
Le mélange à deux corps
Ces deux corps peuvent être deux atomes A et B d’un alliage métallique (Al et Cu, Fe et C…), ou deux molécules d’un mélange de gaz (O2 et N2…). Nous utilisons les perles vertes et bleues pour les représenter. Nous travaillons dans le volume constant de notre rectangle.
Lors du mélange des deux corps, des effets énergétiques et des effets entropiques se manifestent :
Effets énergétiques : ils résultent des interactions entre les atomes A et B. Autrement dit : que préfèrent les atomes A ? Etre entourés d’atomes A ou être voisins d’atomes B ? Ce sont évidemment des effets importants pour prédire le résultat du mélange. Les potentiels interatomiques sont une bonne approximation de ces interactions. On les note : UAA, UBB et UAB.
-
-
- Si UAB > (UAA + UBB)/2, les atomes A et B n’ont pas intérêt à se mélanger
- Si UAB < (UAA + UBB)/2, les atomes A et B ont intérêt à se mélanger ; leur énergie potentielle en étant mélangés est plus basse.
-
Effets entropiques : on montre que l’entropie de mélange des deux corps A et B où c est la concentration en atomes B et (1-c) est la concentration en atomes A (c= nombre d‘atomes B avec N le nombre total d’atomes A + B) est :
![]()
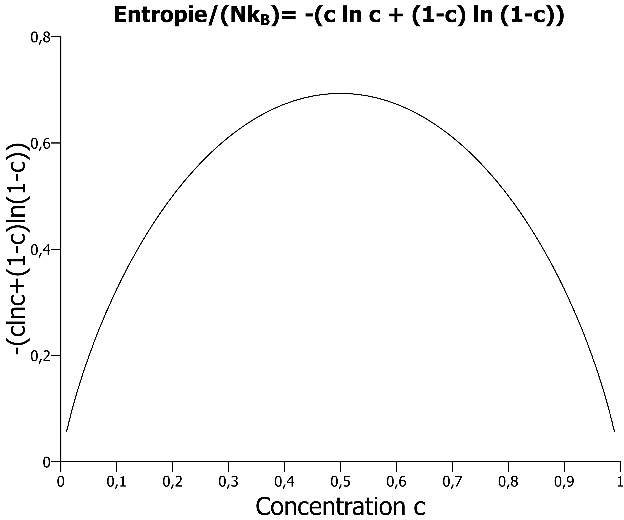
Entropie d’un mélange de deux corps en fonction de la concentration c. L’entropie est de 0 pour les corps purs (c=0 et c=1) et elle est maximale pour le mélange de composition 50/50.
Le bilan entre effets énergétiques et effets entropiques est représenté dans la fonction de Helmholtz A = U – TS. Calculons l’énergie interne U : pour cela on ne tient compte que des énergies d’interaction entre proches voisins UAA, UBB et UAB.
N(1-c) est le nombre d’atomes A et Nc est le nombre d’atomes B. Si Z est la coordinence, c’est-à-dire le nombre de voisins qui entourent chaque atome A ou B, alors le nombre de paires (A,B) est N(1-c)Zc, le nombre de paires (A,A) est (1/2)N(1-c)Z(1-c) = (1/2)NZ(1-c)2 et le nombre de paires (B,B) est (1/2)NcZc = (1/2)NZc2. L’énergie interne du mélange est donc :
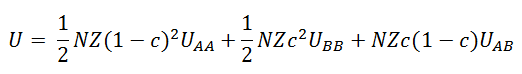 Expression que nous réduisons à :
Expression que nous réduisons à :
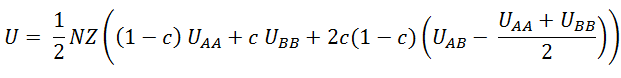 ξ est le facteur qui compare l’énergie d’interaction UAB à la moyenne des énergies d’interaction UAA et UBB . Lorsque ξ est positif, les atomes A préfèrent s’entourer d’atomes B que d’atomes A (idem pour B) :
ξ est le facteur qui compare l’énergie d’interaction UAB à la moyenne des énergies d’interaction UAA et UBB . Lorsque ξ est positif, les atomes A préfèrent s’entourer d’atomes B que d’atomes A (idem pour B) :
![]()
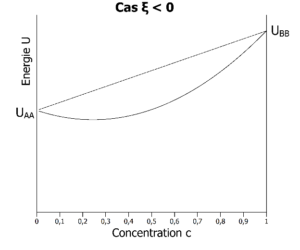
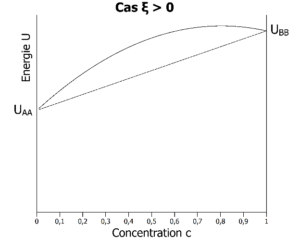
La fonction de Helmholtz peut donc être représentée graphiquement ci-dessous.
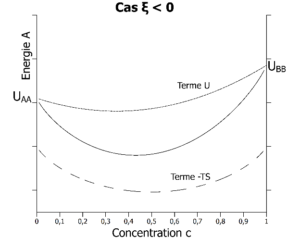
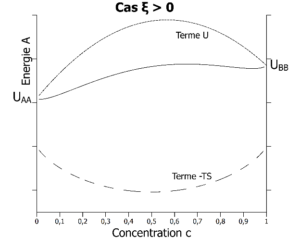
Energie libre (fonction de Helmholtz si V est constant ou de Gibbs si P est constant) à la température T dans les 2 cas possibles : à gauche, A préfère s’entourer de B (ξ < 0). A droite, A préfère s’entourer de A (ξ > 0). A gauche, les atomes A seront intimement mélangés aux atomes B quelle que soit la concentration en atomes A. A droite, les atomes A vont se séparer des atomes B au-delà d’une certaine concentration en atomes A.
Nous avons donc calculé la fonction de Helmholtz du mélange intime A,B à toutes concentrations. La question que nous pouvons nous poser maintenant est : ce mélange intime est-il stable à toute concentration ? Il se peut qu’à certaines concentrations, la séparation du mélange en deux phases de concentrations c1 et c2 soit plus stabilisante que le mélange intime, car l’énergie A est plus basse. En nous posant cette question nous recherchons l’état d’équilibre* de notre alliage, c’est-à-dire la ou les phases qui minimisent l’énergie A. C’est le principe du calcul des diagrammes de phase.
*le plus stable
Les diagrammes de phase
Diagramme de phase du mélange à deux corps
Nous venons de calculer l’énergie A de l’alliage monophasé, constitué du mélange intime A et B. Pour comparer cette énergie à la situation diphasée nous devons calculer la fonction de Helmholtz de l’alliage diphasé. On note α et β les deux phases de concentrations c1 et c2 en atomes B. Ces deux phases se trouvent elles-mêmes dans les proportion x (pour la phase β) et 1-x (pour la phase α) avec :
x= nombre d‘atomes dans la phase / β Nombre total d’atomes
L’énergie A de l’alliage diphasé est A=(1-x)A1+xA2.
Nous pouvons donc maintenant comparer les deux situations. Si ξ est négatif, où si la température est suffisamment élevée pour que le terme entropique l’emporte à toute concentration sur le terme énergétique, nous avons miscibilité totale : le mélange est intime à toute concentration. L’alliage est monophasé. La phase « mélange intime » prend toutes les concentrations et représente toujours l’état d’équilibre.
Si ξ est positif et la température assez basse, à partir d’une certaine concentration c > c1, l’alliage va diminuer son énergie A en se séparant en deux phases de compositions c1 et c2. On parle de démixtion.
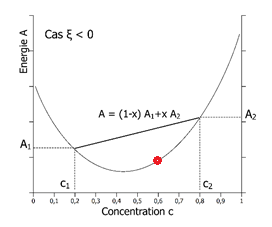
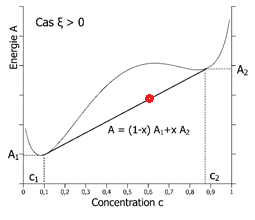


A gauche, cas du mélange stable de composition globale c = 60% (0.6) : l’énergie A du mélange intime (courbe) est toujours plus basse que l’énergie de deux phases séparées (toute droite reliant deux point c1 et c2). A droite, cas du mélange instable de composition globale c = 60% (0.6), conduisant à la séparation de phase : l’énergie A des deux phases séparées de composition c1 = 0.1 et c2 = 0.9 est plus basse que l’énergie A du mélange intime (courbe).
En plus de la composition c du mélange (A,B), on voit que les deux paramètres essentiels sont le paramètre ξ pour les effets énergétiques et T pour les effets entropiques. Le diagramme de phase donne les domaines d’existence du mélange monophasé ou du mélange diphasé en fonction de la température et de la composition. La courbe frontière du domaine diphasé donne les compositions des deux phases en présence.
Les diagrammes de phase existent pour un très grand nombre d’alliages métalliques et de mélange d’oxydes. Ce sont des outils très importants pour prévoir les phases en présence et les microstructures des matériaux.
Quelques diagrammes de phase d’importance économique
Le potentiel chimique
Dans le mélange (A,B), le potentiel chimique de A, µA, est la contribution des atomes A à l’énergie de Gibbs du mélange, G :
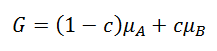
Le potentiel chimique est utile quand on s’intéresse au comportement d’un élément ou d’une espèce chimique en particulier. Par exemple, il aide à prévoir les phénomènes de diffusion chimique et de réactivité. On montre que le potentiel chimique d’un élément est relié à sa concentration dans le mélange, moyennant un coefficient appelé coefficient d’activité dans lequel on met les effets énergétiques. La règle générale est qu’à l’équilibre, le potentiel chimique de A doit être le même dans toutes les phases en présence qui contiennent A. Si ce n’est pas le cas, il faut s’attendre à ce que l’élément A diffuse ou se transforme (se combine avec d’autres éléments) pour diminuer et égaliser son potentiel chimique.
