La chaleur est de l’énergie à l’état dispersé, stockée dans les mouvements atomiques et moléculaires à très petite échelle. Dans un gaz ou dans un liquide, elle est produite par les translations des molécules dans toutes les directions, par les vibrations et par les rotations de ces molécules. La température est reliée à la vitesse de ces déplacements thermiques. Pour un mouvement de vibration, elle est donc aussi reliée à l’amplitude de la vibration (plus l’amplitude est grande et plus la vitesse lors du passage de la position d’équilibre est grande).
Dans un solide, les atomes ne sont pas fixes ! Ils sont animés d’importants mouvements de vibration. Quand un corps solide s’échauffe, les électrons les plus externes sont promus dans des niveaux d’énergie supérieurs (quand il y en a) et l’amplitude des vibrations augmente. Parfois quelques atomes, parmi les plus faiblement liés, vont parvenir à se déplacer sur de grandes distances lorsque l’amplitude de leurs vibrations est suffisante pour les faire sortir de leur position d’équilibre et tomber dans une autre position d’équilibre vacante. C’est le phénomène de diffusion chimique.
Les propriétés thermiques ne sont pas toujours explicitement présentes dans le cahier des charges d’un matériau (hormis les matériaux pour la conduction ou l’isolation thermique), pourtant elles sont toujours importantes, car il y a toujours un domaine de température de fonctionnement du matériau et elles participent à de nombreuses qualités sensorielles. Trois propriétés sont fondamentales : la dilatation thermique, la conductivité thermique et la capacité calorifique.
La dilatation thermique
Dans un solide, par définition, la chaleur est stockée uniquement dans les mouvements de vibration. Il n’y a pas de changements de configuration atomique, ces mouvements à longue distance présents dans les corps qui « coulent ».
Un atome vibre autour de sa position d’équilibre parce qu’il est soumis à des forces de rappel produites par les liaisons chimiques. Comme on l’a vu dans la section sur l’ordre et la structure, qu’elles soient de nature ionique, métallique ou covalente, les liaisons entre atomes peuvent toujours être modélisées par des courbes de potentiel interatomique en première approximation.
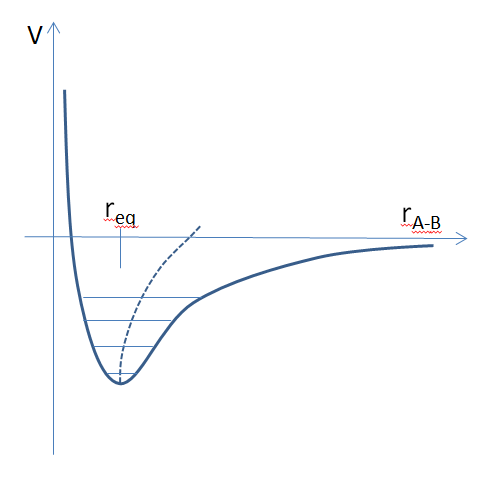
Potentiel interatomique représentant la liaison entre un atome A et un atome B. rA-B est la distance entre les 2 atomes, req représente la position d’équilibre. Lorsque la distance rA-B varie, l’énergie potentielle V augmente. Les énergies quantifiées de vibration, ou « niveaux vibrationnels », sont représentées par les traits horizontaux. Le solide stocke de la chaleur en occupant des niveaux vibrationnels de plus en plus élevés. L’amplitude de vibration augmente (c’est la longueur des traits horizontaux). La distance rA-B moyenne est figurée par la ligne pointillée, son augmentation avec la température est à l’origine de la dilatation.
Le potentiel interatomique réel n’est jamais symétrique autour de la position d’équilibre : il s’affaiblit à grande distance quand les atomes ne se ressentent plus mutuellement. A cause de cela, la distance interatomique moyenne augmente avec la température, c’est la dilatation.
Ce phénomène est universel mais on voit que selon le type de liaison chimique, les puits de potentiel sont plus ou moins profonds et symétriques et la dilatation va être très variable. Se rajoutent à cela les effets de la structure atomique et de la microstructure. Certaines structures cristallines ont une dilatation fortement anisotrope : les atomes s’éloignent beaucoup dans une direction mais en moyenne se rapprochent dans une autre. C’est le cas des cristaux aluminosilicates formés dans les vitrocéramiques à faible coefficient de dilatation : leur distribution homogène et leur orientation aléatoire au sein de la phase vitreuse font qu’à l’échelle du matériau, la dilatation est pratiquement nulle. Ces matériaux sont très utiles dans les applications où il faut une grande stabilité mécanique malgré de fortes variations de température : inserts de cheminée, plaques de cuisson, mais aussi hublots de navettes spatiales, miroirs de téléscopes…
Les métaux et les polymères se dilatent beaucoup de façon générale, car les liaisons métallique et intermoléculaire ne correspondent pas à des puits de potentiel profonds. Les solides iono-covalents se dilatent moins en comparaison.
[tableau de propriétés]
La conductivité thermique
La conductivité thermique κ mesure le flux de chaleur qui traverse le matériau soumis à une différence de température sur ses deux faces :
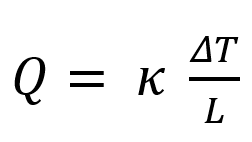
Q est le flux de chaleur en W.m-2, ΔT est la différence de température entre les deux faces du matériau en Kelvin K, L est l’épaisseur de la lame de matériau et κ est la conductivité thermique en W.m-1.K-1.
La résistance thermique mesure la résistance d’un matériau au transfert de chaleur. Pour une lame de matériau d’épaisseur L, elle vaut
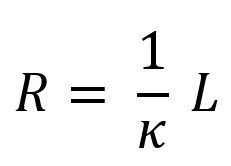
Il existe trois modes de transfert de chaleur qui peuvent être actifs tous les trois au sein d’un matériau :
- La conduction est le transfert de chaleur par le biais de la propagation du mouvement des atomes les uns aux autres, de proche en proche à travers les liaisons chimiques.
- La convection est le transfert par les mouvements à grande distance de grandes quantités d’atomes, dans l’air ou dans les liquides
- Le rayonnement est le transfert par absorption d’énergie lumineuse, qui est restituée par les vibrations atomiques.
Parce qu’ils sont denses, la conduction est le mode principal de transfert dans les solides. Sur la face chaude du solide, les vibrations des atomes sont très amples. Les liaisons chimiques transmettent de proche en proche cette amplitude de vibration jusqu’à la face froide. Les ondes de propagation de l’amplitude de vibration d’un atome à l’autre sont appelées « phonons ». La transmission est d’autant plus efficace que ces ondes peuvent parcourir de longues distances à travers le solide grâce au réseau de liaisons chimiques couplées. On parle de « conductivité thermique de réseau », KR.
Dans les métaux, les électrons libres de se déplacer contribuent aussi à la conductivité thermique. Cette contribution est appelée « conductivité thermique électronique », Ke, de sorte que les deux contributions s’additionnent : K = KR + Ke.
Dans les matériaux non-métalliques où la conductivité thermique de réseau est dominante, la conductivité macroscopique (celle mesurée à l’échelle du matériau) est très dépendante du degré d’ordre ou de désordre du matériau de l’échelle atomique à sa microstructure. Dans un cristal parfait, la symétrie translatoire induit une continuité parfaite du réseau de liaisons chimiques et les phonons s’étendent à travers tout le cristal, ils sont « délocalisés ». La conductivité thermique est optimale. Si le cristal présente des défauts tels que des impuretés, des lacunes, des dislocations…, l’amplitude de vibration ne peut plus se propager efficacement, les phonons sont diffusés ou se localisent et la conductivité thermique diminue. Enfin si le même composé se présente sous la forme d’une céramique dont les grains cristallins sont très fins, la conductivité thermique est amoindrie car les phonons s’étendent jusqu’aux limites du grain et l’amplitude de vibration a du mal à être transmise aux grains voisins.
Dans les métaux, même si une toute petite partie seulement des électrons est libre, leur amplitude de déplacement se propage extrêmement rapidement à travers le solide. La contribution électronique domine la conductivité thermique de sorte que les métaux et alliages sont des conducteurs thermiques « par les électrons ». Il y a donc une étroite relation entre conductivité électronique et conductivité thermique : le cuivre pur, un des meilleurs conducteurs électroniques, est aussi un des meilleurs conducteurs thermiques. Cependant le diamant, parfaitement isolant, est encore meilleur conducteur thermique par son réseau !
Tous les solides denses ont donc une relativement bonne conductivité thermique. Pour isoler thermiquement un corps ou un bâtiment, on recourt à des couvertures, du double vitrage, des matériaux poreux… bref, essentiellement à de l’air piégé dans des cavités ! Dépourvu des mécanismes de convection et de conduction, l’air statique est le meilleur isolant.

Microstructure du plâtre (échelle 10 µm, image MEB) : l’enchevêtrement des cristaux en forme d’aiguilles crée une grande porosité à l’origine d’une faible conductivité thermique (K du plâtre = 0.4 W.m-1.K-1 environ)

Chènevotte : particules de bois issues de la tige du chanvre. L’enchevêtrement des tiges piège de l’air. De plus, les tiges de cette plante sont elles-mêmes très poreuses, car constituées de tubes capillaires dont le rôle est de faire monter la sève. En liant les tiges de chanvre avec de la chaux, on obtient un « béton de chanvre » très isolant (K =).
La capacité calorifique et l’inertie thermique
La capacité calorifique massique est la quantité de chaleur qu’il faut apporter à 1 kg de la substance pour élever sa température de 1°C. Elle mesure donc la « capacité de stockage d’énergie désordonnée » dans les différents mouvements atomiques et moléculaires de la substance. A pression ambiante, la quantité de chaleur apportée correspond à la variation d’enthalpie dH dans la matière et la capacité calorifique s’écrit :
Son unité est le J.kg-1.K-1
Bénéficiant d’une grande liberté de mouvements à l’échelle atomique, les liquides et les gaz ont une capacité calorifique plus élevée que les solides, de manière générale. C’est pour cela qu’on utilise des fluides, souvent l’air ou l’eau, pour refroidir une installation qui génère de la chaleur (circuits électriques, réacteurs, etc). Leur capacité calorifique est quasiment indépendante de la température.
Dans la plupart des solides denses, les seuls mouvements atomiques possibles sont les vibrations de réseau ou « phonons ». Il faut un minimum d’énergie thermique pour exciter ces phonons, à cause de la nature quantifiée des échanges d’énergie à cette échelle. C’est pourquoi la capacité thermique est d’abord très basse puis elle augmente avec la température, au fur et à mesure que de plus en plus de phonons sont excités. On définit ainsi la température de Debye : température à partir de laquelle on admet que tous les phonons de la matière sont excités. Dans les solides dont les atomes constitutifs sont légers, et/ou les liaisons chimiques sont fortes, les énergies de phonons sont grandes (ce qui revient à dire que les fréquences et vitesses de ces vibrations sont grandes). Il faut donc élever la température pour pouvoir les exciter et la température de Debye de ces solides est élevée.
Au-delà de la température de Debye, lorsque toutes les vibrations possibles sont excitées, la capacité calorifique prend la valeur universelle de 3R par mole d’atome, soit 25 J.mol-1.K-1. (parfois un peu plus du fait de la contribution des électrons). C’est la limite de Dulong et Petit. Cette loi traduit le principe de l’équipartition de l’énergie : chaque atome porte sa part d’énergie thermique à raison de 3 degrés de liberté par atome (les directions x, y et z de l’espace).
Par conséquent, la capacité calorifique à température ambiante dépend du nombre d’atomes dans un kg et de la température de Debye du solide considéré. Le plomb a une capacité calorifique massique à 25°C très faible car il est très lourd, mais sa capacité calorifique molaire est de 25.6 J.mol-1.K-1 donc à la limite de Dulong et Petit. Le beryllium et le bore sont des solides covalents très légers, leur température de Debye est très élevée (plus de 1000 K) et leur capacité calorifique molaire est plus basse que la limite de Dulong et Petit (environ 20 J.mol-1.K-1). Comme ils sont légers, leur capacité massique est pourtant plus grande que celle du plomb (il y a 40 fois plus d’atomes dans un kg de beryllium que dans un kg de plomb).
La capacité calorifique est une propriété importante des matériaux de construction car elle est reliée à l’inertie thermique du bâtiment, très importante pour le confort d’été. Les matériaux à forte capacité calorifique stockent la chaleur pendant les heures chaudes et la restituent lentement pendant les heures fraîches, induisant à la fois un déphasage et un amortissement des variations de température à l’intérieur du bâtiment. La capacité calorifique volumique est une mesure directe de l’inertie thermique apportée par un matériau, qui tient compte de sa masse volumique :
Cp volumique = Cp massique X masse volumique
Les Cp massiques étant relativement proches pour les différentes matières utiles à la construction, plus un mur est épais et dense (peu poreux), plus son inertie thermique est grande. C’est le cas des vieilles maisons en terre ou en pierres. On voit aussi que les matériaux poreux sont de très bons isolants thermiques mais confèrent très peu d’inertie thermique.
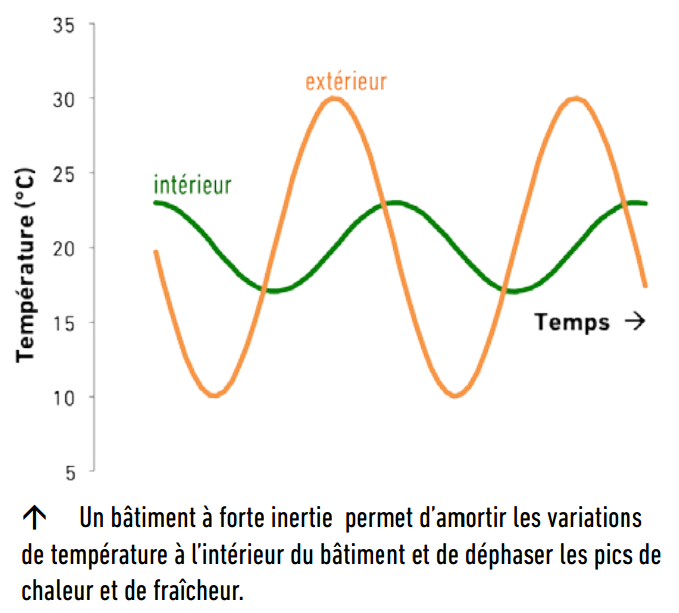
Extrait de la synthèse du projet « Béton d’Argile Environnemental », CRATerre-ENSAG, MATEIS-INSA de Lyon, DGCB-ENTPE.
